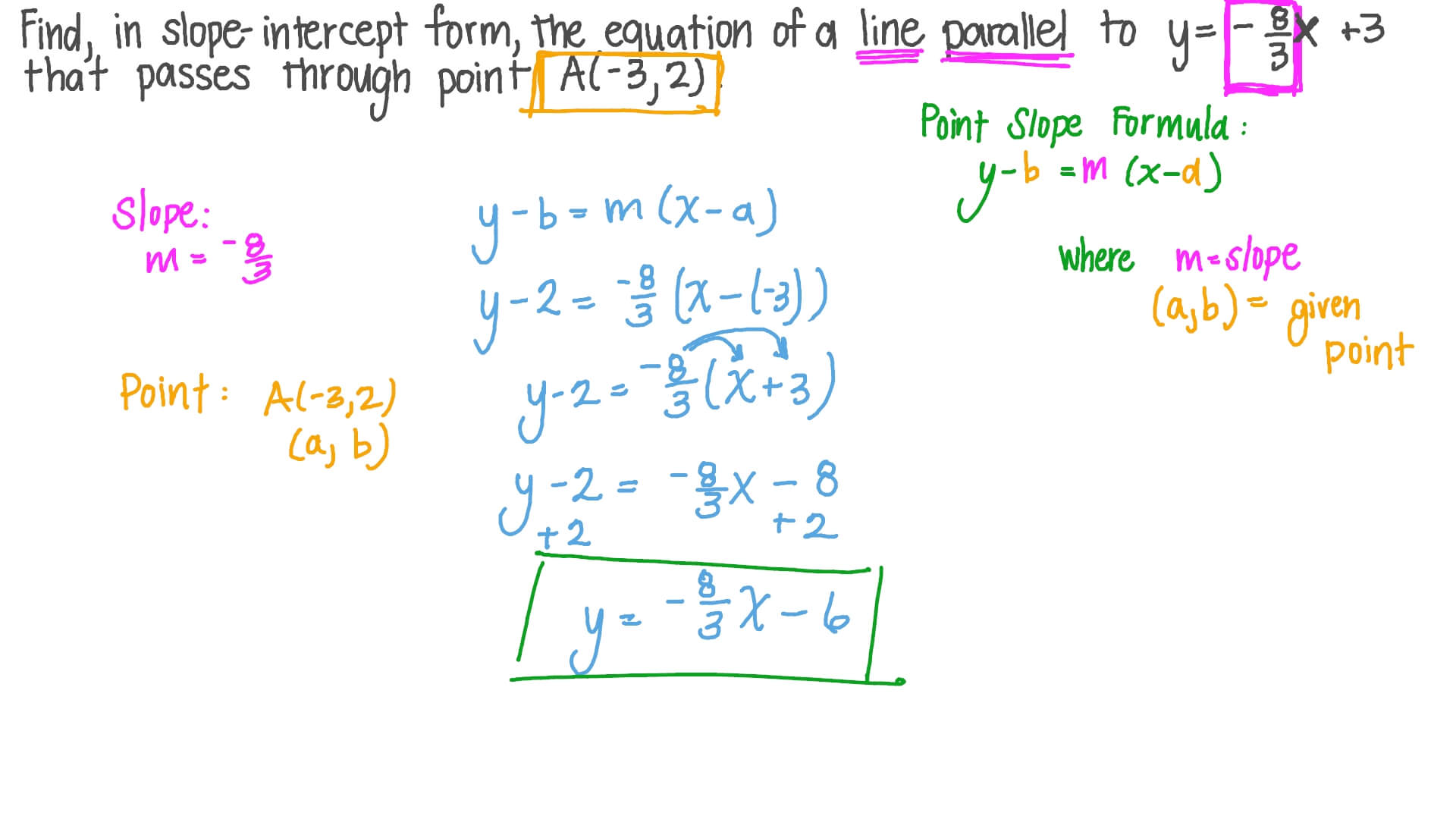Parallel Lines Slope Intercept Form
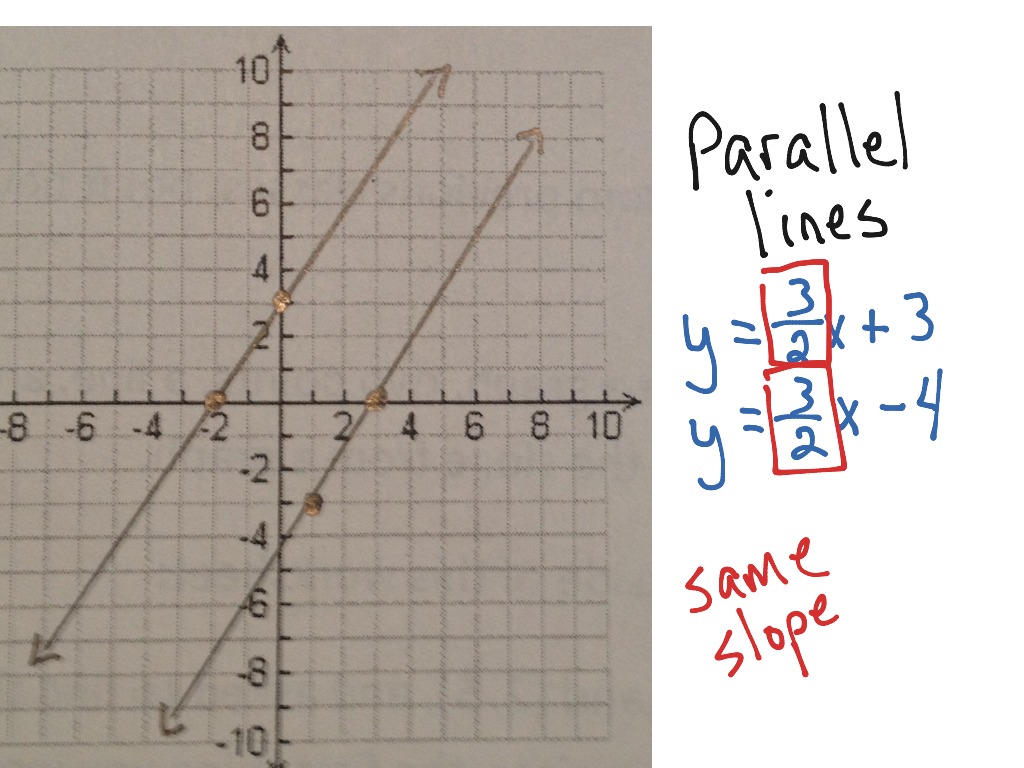
Parallel Lines Slope Intercept Form - \large y=\maroonc {m}x+\greene {b} y = mx + b here, \maroonc {m} m and \greene {b} b can be any two real numbers. Since, both equation have same slope therefore these two equation part ii and part i are parallel. Watch this video to learn more about it and see some examples. The given equation of a line is y = 2x + 3. Divide both sides by 8. Where # (x_1,y_1)# and # (x_2,y_2)# are the coordinates of any two points in the line. Web find the equation of the line that is: The lines are parallel if their slopes are equal or the same. There are various forms which we can write the equation of a. The slope of the line, #m#, is found by.
If you can find the slope of that parallel line, you'll have the slope of your line! If you rewrite the equation of the line in standard form ax+by=c, the distance can be calculated as: There are various forms which we can write the equation of a. Here is a common format for exercises on this topic: Taken another equation of line part ii= whose slope of line part ii is m=1/2. It has the following general structure. The given equation of a line is y = 2x + 3. Since, both equation have same slope therefore these two equation part ii and part i are parallel. Parallel lines have the same slope proof: Perpendicular lines have opposite reciprocal slopes analytic geometry faq math > high school geometry > analytic geometry > equations of parallel & perpendicular lines © 2023 khan academy terms of use privacy policy cookie notice parallel lines from equation ccss.math:
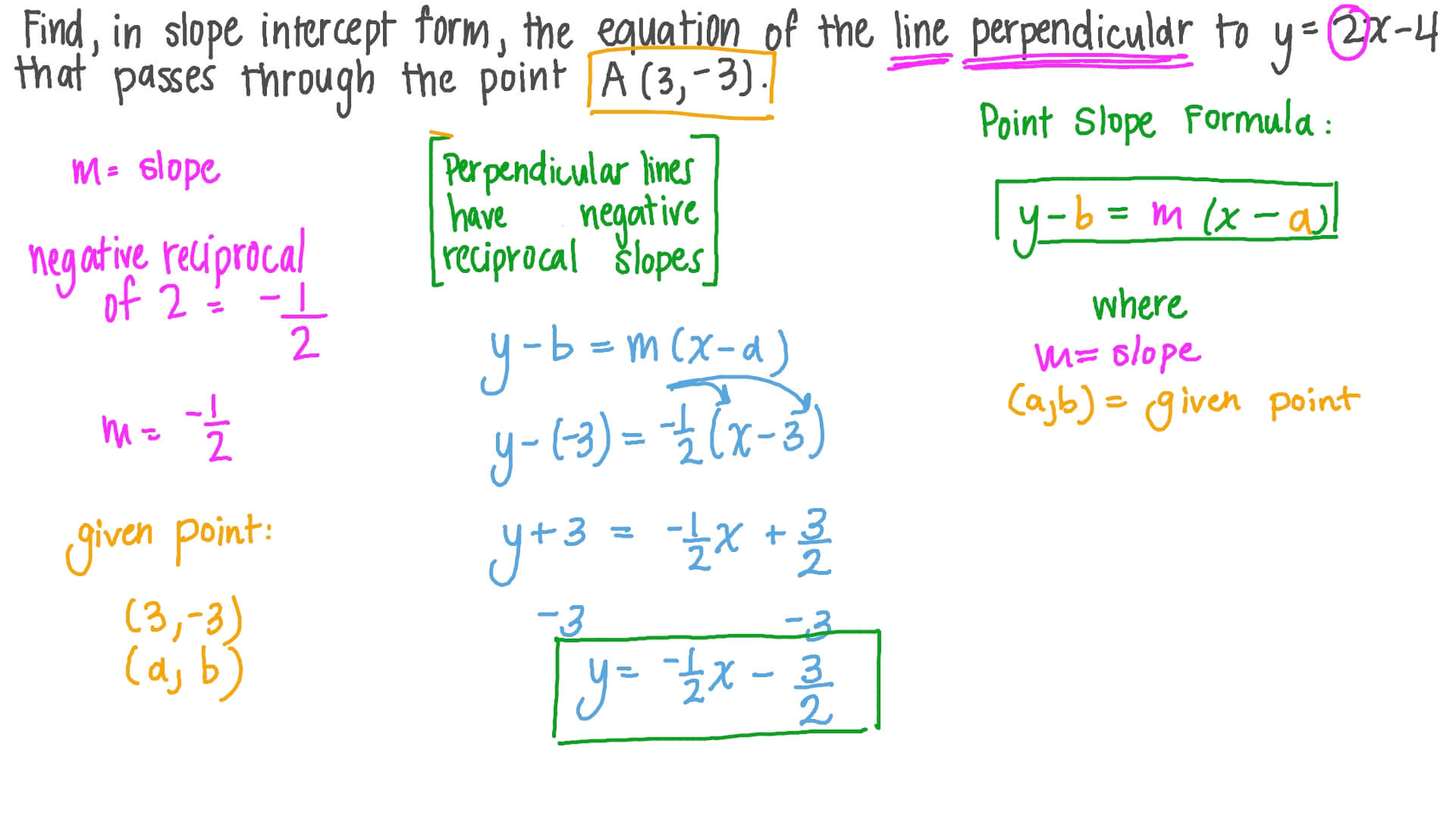
We can do the same thing for perpendicular lines. Web first, you should put the equation in slope intercept form (y = mx + b), where m is the slope. Y − 4 = 2 (x − 5) that is an answer! Finding parallel and perpendicular lines. Parallel lines have the same slope proof: \large y=\maroonc {m}x+\greene {b} y = mx + b here, \maroonc {m} m and \greene {b} b can be any two real numbers. Here is a common format for exercises on this topic: Part i= equation of line. Y − y1 = 2 (x − x1) and then put in the point (5,4): The slope of the line part i is m=1/2.
Equations of Parallel Lines CK12 Foundation
Parallel lines have the same slope proof: Web the equation of a line is such that its highest exponent on its variable (s) is 1. Web remember, parallel lines have the same slope. Y − 4 = 2 (x − 5) that is an answer! Finding parallel and perpendicular lines.
Equations of Parallel Lines CK12 Foundation
Watch this video to learn more about it and see some examples. Part i= equation of line. Top voted camron williams 5 years ago It has the following general structure. There are various forms which we can write the equation of a.
Finding the slopes of lines parallel or perpendicular to a given line
The slope of the line, #m#, is found by. There are various forms which we can write the equation of a. \large y=\maroonc {m}x+\greene {b} y = mx + b here, \maroonc {m} m and \greene {b} b can be any two real numbers. Compare these values to the equation y = mx + b. If you rewrite the equation.
Parallel or Perpendicular Lines in Standard and Slope Intercept Form
Web we have given that: Web first, you should put the equation in slope intercept form (y = mx + b), where m is the slope. We can do the same thing for perpendicular lines. Top voted camron williams 5 years ago Review related articles/videos or use a hint.
Parallel lines and slope Math ShowMe
#m# is the slope of the equation. We can do the same thing for perpendicular lines. Questions tips & thanks want to join the conversation? Here is a common format for exercises on this topic: If you rewrite the equation of the line in standard form ax+by=c, the distance can be calculated as:
Question Video Finding in SlopeIntercept Form the Equation of
There are no exponents in its variable (s)). Web first, you should put the equation in slope intercept form (y = mx + b), where m is the slope. Web we have given that: The slope of the line, #m#, is found by. Web the equation of a line is such that its highest exponent on its variable (s) is.
Slope Intercept Form With Parallel Lines Simple Guidance For You In
Perpendicular lines have opposite reciprocal slopes analytic geometry faq math > high school geometry > analytic geometry > equations of parallel & perpendicular lines © 2023 khan academy terms of use privacy policy cookie notice parallel lines from equation ccss.math: Web we have given that: The slope of the line, #m#, is found by. Part i= equation of line. Challenge.
Parallel Slopes and Perpendicular Slopes Complete Guide — Mashup Math
Review related articles/videos or use a hint. It has the following general structure. Divide both sides by 8. Compare these values to the equation y = mx + b. Web any linear equation has the form of.
Slope Intercept Form Write Equation from Two Known Points Expii
Web find the equation of the line that is: Divide both sides by 8. Top voted camron williams 5 years ago Where # (x_1,y_1)# and # (x_2,y_2)# are the coordinates of any two points in the line. #m# is the slope of the equation.
Slope Of A Parallel Line slide share
Web the equation of a line is such that its highest exponent on its variable (s) is 1. Slope intercept form is y=mx+c. Where # (x_1,y_1)# and # (x_2,y_2)# are the coordinates of any two points in the line. There are various forms which we can write the equation of a. Finding parallel and perpendicular lines.
Web First, You Should Put The Equation In Slope Intercept Form (Y = Mx + B), Where M Is The Slope.
Part i= equation of line. Slope intercept form is y=mx+c. Web remember, parallel lines have the same slope. Y − 4 = 2 (x − 5) that is an answer!
Challenge Yourself In The Line Game!
#m# is the slope of the equation. Web the equation of a line is such that its highest exponent on its variable (s) is 1. Watch this video to learn more about it and see some examples. Taken another equation of line part ii= whose slope of line part ii is m=1/2.
It Is Also Shown By The Graph Attached.
The given equation of a line is y = 2x + 3. Perpendicular lines have opposite reciprocal slopes analytic geometry faq math > high school geometry > analytic geometry > equations of parallel & perpendicular lines © 2023 khan academy terms of use privacy policy cookie notice parallel lines from equation ccss.math: Where # (x_1,y_1)# and # (x_2,y_2)# are the coordinates of any two points in the line. Since, both equation have same slope therefore these two equation part ii and part i are parallel.
Here Is A Common Format For Exercises On This Topic:
Questions tips & thanks want to join the conversation? Parallel lines have the same slope, to find the parallel line at a given point you should simply calculate the. Y − y1 = 2 (x − x1) and then put in the point (5,4): Parallel lines have the same slope proof: