Find Component Form Of Vector
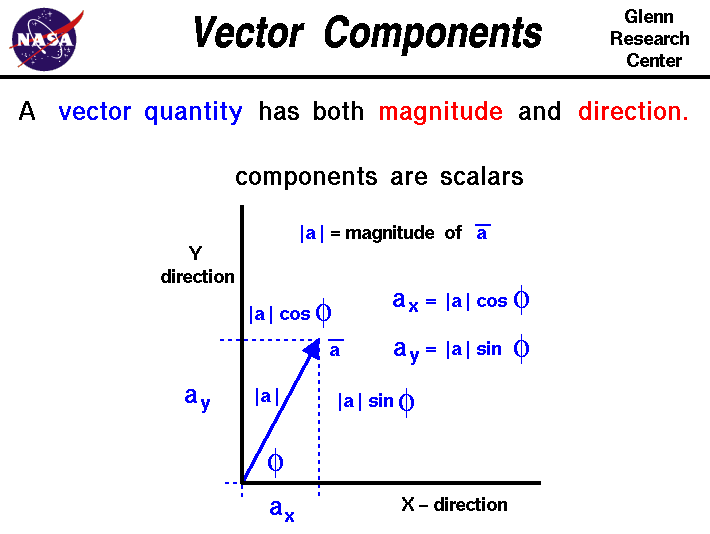
Find Component Form Of Vector - Web this is the component form of a vector. Plug in the x, y, and z values of the initial and terminal points into the component form formula. Find the component form of the specified vector. Web the component form of the vector from the point a = (5,8) to the origin is o. The component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down. (simplify your answers.) this problem has been solved! Here, x, y, and z are the scalar components of \( \vec{r} \) and x\( \vec{i} \), y\( \vec{j} \), and z\( \vec{k} \) are the vector components of \(. Web 316k views 9 years ago vectors. Web when given the magnitude (r) and the direction (theta) of a vector, the component form of the vector is given by r (cos (theta), sin (theta)). Web the component form of vector ab with a(a x, a y, a z) and b(b x, b y, b z) can be found using the following formula:
A vector is defined as a quantity with both magnitude and. Web answer (1 of 2): Web to find the magnitude of a vector from its components, we take the square root of the sum of the components' squares (this is a direct result of the pythagorean theorem): The component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down. How do we use the components of two vectors to find the resultant vector by adding the two vectors ? {eq}v_y = ||v||\sin \theta {/eq} step 3: Identify the initial point and the terminal point of the vector. Web the component form of vector ab with a(a x, a y, a z) and b(b x, b y, b z) can be found using the following formula: {eq}v_x = ||v||\cos \theta {/eq} step 2: Web 316k views 9 years ago vectors.
Web this is the component form of a vector. Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in. (simplify your answers.) this problem has been solved! Web answer (1 of 2): Web 316k views 9 years ago vectors. Here, x, y, and z are the scalar components of \( \vec{r} \) and x\( \vec{i} \), y\( \vec{j} \), and z\( \vec{k} \) are the vector components of \(. Web to find the magnitude of a vector from its components, we take the square root of the sum of the components' squares (this is a direct result of the pythagorean theorem): Find the component form of the specified vector. Identify the initial point and the terminal point of the vector. Web the component form of the vector from the point a = (5,8) to the origin is o.
Vector Components
{eq}v_x = ||v||\cos \theta {/eq} step 2: Web the component form of vector ab with a(a x, a y, a z) and b(b x, b y, b z) can be found using the following formula: How do we use the components of two vectors to find the resultant vector by adding the two vectors ? Web this is the component.
How to write component form of vector
Web to find the magnitude of a vector from its components, we take the square root of the sum of the components' squares (this is a direct result of the pythagorean theorem): Identify the initial point and the terminal point of the vector. The coefficients of the unit vectors are the projections of the vector onto those unit vectors (found.
How To Find Component Form Of A Vector Given Initial And Terminal Points
How do we use the components of two vectors to find the resultant vector by adding the two vectors ? The coefficients of the unit vectors are the projections of the vector onto those unit vectors (found by taking the cosine of smaller angle formed by the vector and. Web when given the magnitude (r) and the direction (theta) of.
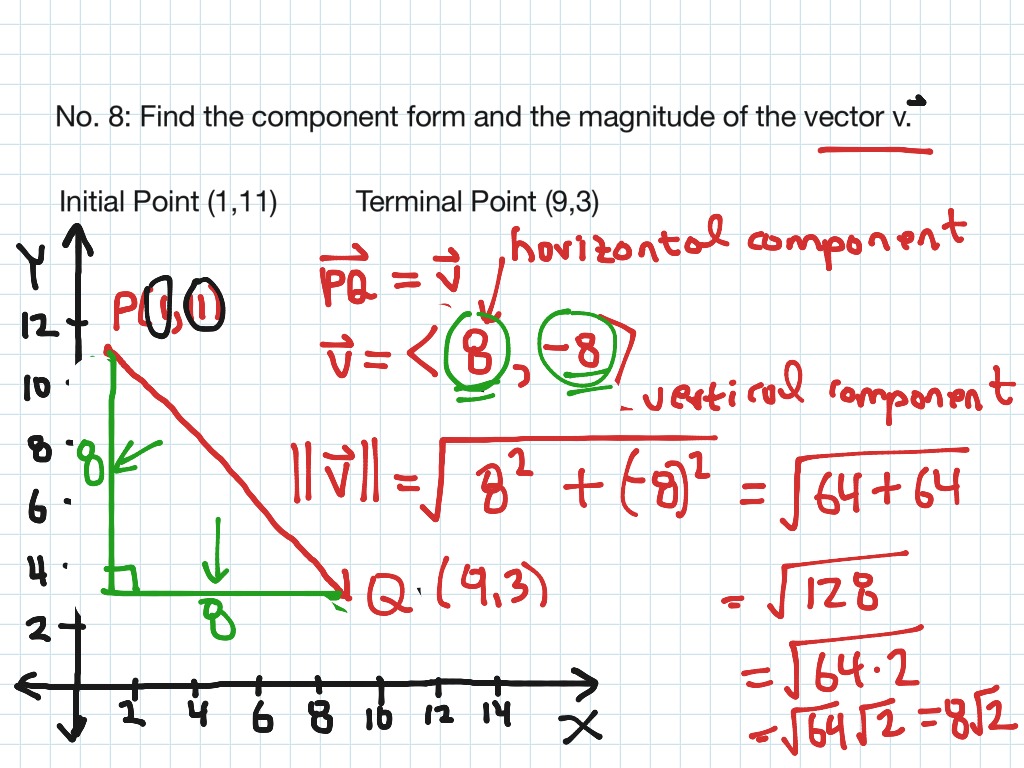
6.3 No. 8 Finding the Component Form and the Magnitude of a Vector
The component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down. A vector is defined as a quantity with both magnitude and. Find the component form of the specified vector. How do we use the components of two.
Order Essay from Experienced Writers with Ease how to write component
Web component form of a vector. How do we use the components of two vectors to find the resultant vector by adding the two vectors ? {eq}v_x = ||v||\cos \theta {/eq} step 2: Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in. Web this is.
Component Form Of A Vector
A vector is defined as a quantity with both magnitude and. Web when given the magnitude (r) and the direction (theta) of a vector, the component form of the vector is given by r (cos (theta), sin (theta)). Web 316k views 9 years ago vectors. The component form of a vector is given as < x, y >, where x.
PC 6.3 Notes Example 8 Find the Component Form of a Vector YouTube
Web answer (1 of 2): The magnitude of a vector [math processing error] v is [math processing error] 20 units and the direction of the vector is. Web the component form of the vector from the point a = (5,8) to the origin is o. Here, x, y, and z are the scalar components of \( \vec{r} \) and x\(.
How To Find Component Form Of A Vector Given Magnitude And Direction
Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in. Web when given the magnitude (r) and the direction (theta) of a vector, the component form of the vector is given by r (cos (theta), sin (theta)). Identify the initial point and the terminal point of.
How To Find Component Form Of A Vector Given Magnitude And Direction
{eq}v_y = ||v||\sin \theta {/eq} step 3: (simplify your answers.) this problem has been solved! A vector is defined as a quantity with both magnitude and. Web to find the magnitude of a vector from its components, we take the square root of the sum of the components' squares (this is a direct result of the pythagorean theorem): The coefficients.
Component Vector ( Video ) Calculus CK12 Foundation
Web answer (1 of 2): Find the component form of the specified vector. Plug in the x, y, and z values of the initial and terminal points into the component form formula. How do we use the components of two vectors to find the resultant vector by adding the two vectors ? Web the component form of the vector from.
{Eq}V_Y = ||V||\Sin \Theta {/Eq} Step 3:
Web answer (1 of 2): Web component form of a vector. Web the component form of vector ab with a(a x, a y, a z) and b(b x, b y, b z) can be found using the following formula: The magnitude of a vector [math processing error] v is [math processing error] 20 units and the direction of the vector is.
A Vector Is Defined As A Quantity With Both Magnitude And.
Web the component form of the vector from the point a = (5,8) to the origin is o. Find the component form of the specified vector. Here, x, y, and z are the scalar components of \( \vec{r} \) and x\( \vec{i} \), y\( \vec{j} \), and z\( \vec{k} \) are the vector components of \(. Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in.
Web Improve Your Math Knowledge With Free Questions In Find The Component Form Of A Vector And Thousands Of Other Math Skills.
Web when given the magnitude (r) and the direction (theta) of a vector, the component form of the vector is given by r (cos (theta), sin (theta)). The coefficients of the unit vectors are the projections of the vector onto those unit vectors (found by taking the cosine of smaller angle formed by the vector and. (simplify your answers.) this problem has been solved! Web this is the component form of a vector.
You'll Get A Detailed Solution From A Subject.
Web to find the magnitude of a vector from its components, we take the square root of the sum of the components' squares (this is a direct result of the pythagorean theorem): {eq}v_x = ||v||\cos \theta {/eq} step 2: Identify the initial point and the terminal point of the vector. The component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down.