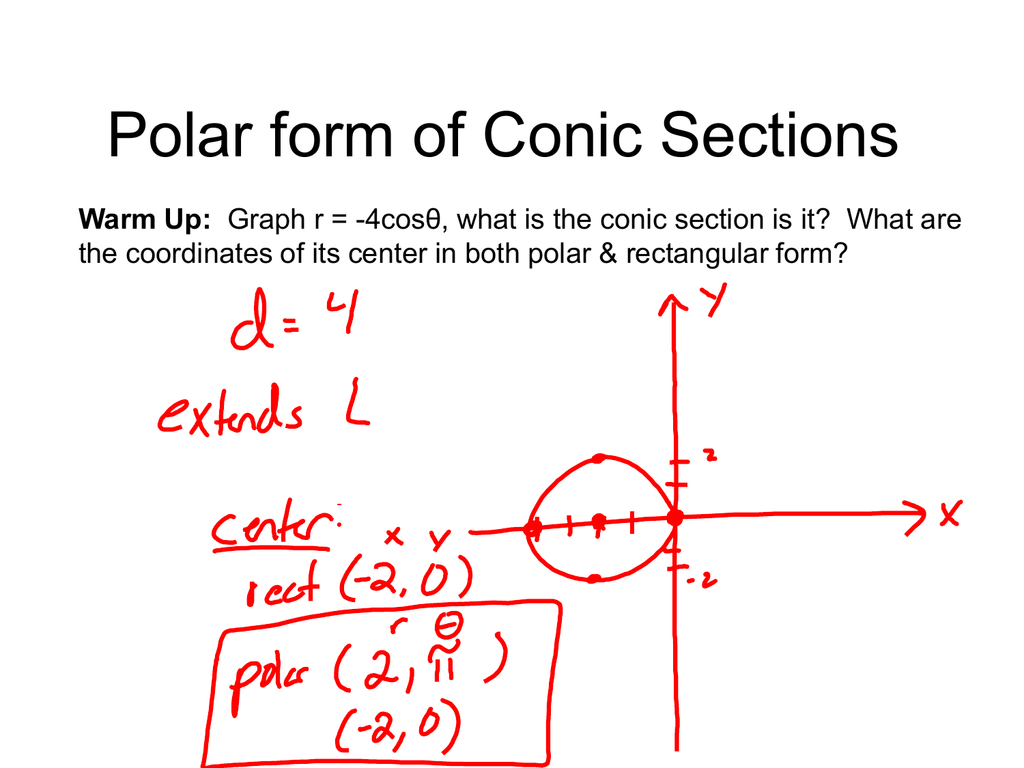
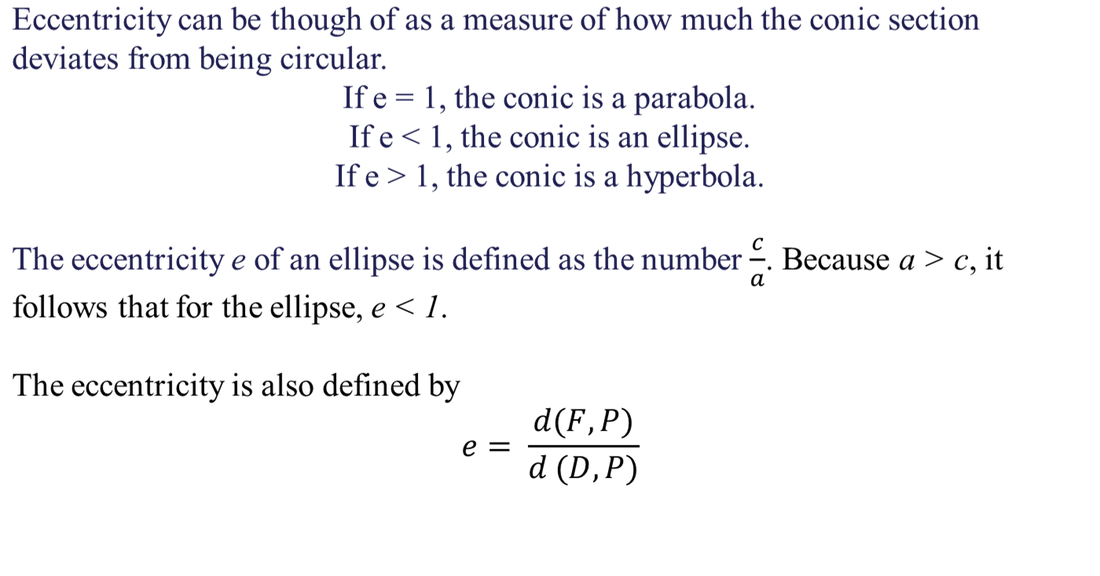Ellipse Polar Form
Ellipse Polar Form - I couldn’t easily find such an equation, so i derived it and am posting it here. The family of ellipses handled in the quoted passage was chosen specifically to have a simple equation in polar coordinates. Pay particular attention how to enter the greek letter theta a. (x/a)2 + (y/b)2 = 1 ( x / a) 2 + ( y / b) 2 = 1. We easily get the polar equation. An ellipse is a figure that can be drawn by sticking two pins in a sheet of paper, tying a length of string to the pins, stretching the string taut with a pencil, and drawing the figure that results. An ellipse can be specified in the wolfram language using circle [ x, y, a , b ]. Figure 11.5 a a b b figure 11.6 a a b b if a < Web the polar form of a conic to create a general equation for a conic section using the definition above, we will use polar coordinates. Rather, r is the value from any point p on the ellipse to the center o.
For now, we’ll focus on the case of a horizontal directrix at y = − p, as in the picture above on the left. Web the ellipse is a conic section and a lissajous curve. Web in this document, i derive three useful results: For the description of an elliptic orbit, it is convenient to express the orbital position in polar coordinates, using the angle θ: R d − r cos ϕ = e r d − r cos ϕ = e. Start with the formula for eccentricity. As you may have seen in the diagram under the directrix section, r is not the radius (as ellipses don't have radii). The family of ellipses handled in the quoted passage was chosen specifically to have a simple equation in polar coordinates. Web in mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. Web an ellipse is the set of all points (x, y) in a plane such that the sum of their distances from two fixed points is a constant.
Web the ellipse is a conic section and a lissajous curve. R 1 + e cos (1) (1) r d e 1 + e cos. This form makes it convenient to determine the aphelion and perihelion of. An ellipse can be specified in the wolfram language using circle [ x, y, a , b ]. Web beginning with a definition of an ellipse as the set of points in r 2 r → 2 for which the sum of the distances from two points is constant, i have |r1→| +|r2→| = c | r 1 → | + | r 2 → | = c thus, |r1→|2 +|r1→||r2→| = c|r1→| | r 1 → | 2 + | r 1 → | | r 2 → | = c | r 1 → | ellipse diagram, inductiveload on wikimedia Web in mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. I couldn’t easily find such an equation, so i derived it and am posting it here. The family of ellipses handled in the quoted passage was chosen specifically to have a simple equation in polar coordinates. Web an ellipse is the set of all points (x, y) in a plane such that the sum of their distances from two fixed points is a constant. Pay particular attention how to enter the greek letter theta a.
Equation For Ellipse In Polar Coordinates Tessshebaylo
Web a slice perpendicular to the axis gives the special case of a circle. Web in an elliptical orbit, the periapsis is the point at which the two objects are closest, and the apoapsis is the point at which they are farthest apart. Pay particular attention how to enter the greek letter theta a. (it’s easy to find expressions for.
Example of Polar Ellipse YouTube
I have the equation of an ellipse given in cartesian coordinates as ( x 0.6)2 +(y 3)2 = 1 ( x 0.6) 2 + ( y 3) 2 = 1. Web the polar form of a conic to create a general equation for a conic section using the definition above, we will use polar coordinates. Represent q(x, y) in polar.
Equation Of Ellipse Polar Form Tessshebaylo
It generalizes a circle, which is the special type of ellipse in. For now, we’ll focus on the case of a horizontal directrix at y = − p, as in the picture above on the left. Represent q(x, y) in polar coordinates so (x, y) = (rcos(θ), rsin(θ)). We easily get the polar equation. (it’s easy to find expressions for.
calculus Deriving polar coordinate form of ellipse. Issue with length
An ellipse is a figure that can be drawn by sticking two pins in a sheet of paper, tying a length of string to the pins, stretching the string taut with a pencil, and drawing the figure that results. For the description of an elliptic orbit, it is convenient to express the orbital position in polar coordinates, using the angle.
Equation For Ellipse In Polar Coordinates Tessshebaylo
Web polar equation to the ellipse; This form makes it convenient to determine the aphelion and perihelion of. I have the equation of an ellipse given in cartesian coordinates as ( x 0.6)2 +(y 3)2 = 1 ( x 0.6) 2 + ( y 3) 2 = 1. Place the thumbtacks in the cardboard to form the foci of the.
Ellipses in Polar Form Ellipses
Web the given ellipse in cartesian coordinates is of the form $$ \frac{x^2}{a^2}+ \frac{y^2}{b^2}=1;\; Pay particular attention how to enter the greek letter theta a. We easily get the polar equation. Web in an elliptical orbit, the periapsis is the point at which the two objects are closest, and the apoapsis is the point at which they are farthest apart..
Ellipse (Definition, Equation, Properties, Eccentricity, Formulas)
The polar form of an ellipse, the relation between the semilatus rectum and the angular momentum, and a proof that an ellipse can be drawn using a string looped around the two foci and a pencil that traces out an arc. Web in an elliptical orbit, the periapsis is the point at which the two objects are closest, and the.
Polar description ME 274 Basic Mechanics II
Web the equation of a horizontal ellipse in standard form is \(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) where the center has coordinates \((h,k)\), the major axis has length 2a, the minor axis has length 2b, and the coordinates of the foci are \((h±c,k)\), where \(c^2=a^2−b^2\). Web in an elliptical orbit, the periapsis is the point at which the two objects are closest, and the apoapsis.
Conics in Polar Coordinates Unified Theorem for Conic Sections YouTube
Start with the formula for eccentricity. Web it's easiest to start with the equation for the ellipse in rectangular coordinates: Web beginning with a definition of an ellipse as the set of points in r 2 r → 2 for which the sum of the distances from two points is constant, i have |r1→| +|r2→| = c | r 1.
Ellipses in Polar Form YouTube
Web formula for finding r of an ellipse in polar form. Figure 11.5 a a b b figure 11.6 a a b b if a < Represent q(x, y) in polar coordinates so (x, y) = (rcos(θ), rsin(θ)). Web in mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the.
(It’s Easy To Find Expressions For Ellipses Where The Focus Is At The Origin.)
R 1 + e cos (1) (1) r d e 1 + e cos. As you may have seen in the diagram under the directrix section, r is not the radius (as ellipses don't have radii). Start with the formula for eccentricity. The polar form of an ellipse, the relation between the semilatus rectum and the angular momentum, and a proof that an ellipse can be drawn using a string looped around the two foci and a pencil that traces out an arc.
Web The Polar Form Of A Conic To Create A General Equation For A Conic Section Using The Definition Above, We Will Use Polar Coordinates.
Generally, the velocity of the orbiting body tends to increase as it approaches the periapsis and decrease as it approaches the apoapsis. Pay particular attention how to enter the greek letter theta a. I have the equation of an ellipse given in cartesian coordinates as ( x 0.6)2 +(y 3)2 = 1 ( x 0.6) 2 + ( y 3) 2 = 1. Generally, the velocity of the orbiting body tends to increase as it approaches the periapsis and decrease as it.
Web The Equation Of A Horizontal Ellipse In Standard Form Is \(\Dfrac{(X−H)^2}{A^2}+\Dfrac{(Y−K)^2}{B^2}=1\) Where The Center Has Coordinates \((H,K)\), The Major Axis Has Length 2A, The Minor Axis Has Length 2B, And The Coordinates Of The Foci Are \((H±C,K)\), Where \(C^2=A^2−B^2\).
Web in this document, i derive three useful results: Web it's easiest to start with the equation for the ellipse in rectangular coordinates: Represent q(x, y) in polar coordinates so (x, y) = (rcos(θ), rsin(θ)). Web ellipses in polar form michael cheverie 77 subscribers share save 63 views 3 years ago playing with the equation of an ellipse in polar form on desmos, the online graphing calculator, by.
Web Beginning With A Definition Of An Ellipse As The Set Of Points In R 2 R → 2 For Which The Sum Of The Distances From Two Points Is Constant, I Have |R1→| +|R2→| = C | R 1 → | + | R 2 → | = C Thus, |R1→|2 +|R1→||R2→| = C|R1→| | R 1 → | 2 + | R 1 → | | R 2 → | = C | R 1 → | Ellipse Diagram, Inductiveload On Wikimedia
I need the equation for its arc length in terms of θ θ, where θ = 0 θ = 0 corresponds to the point on the ellipse intersecting the positive x. An ellipse can be specified in the wolfram language using circle [ x, y, a , b ]. We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string. R d − r cos ϕ = e r d − r cos ϕ = e.