Circulation Form Of Green's Theorem
Circulation Form Of Green's Theorem - His video is all about green's theorem, or at least the first of two green's theorem sometimes called the curl, circulation, or tangential form. A circulation form and a flux form. Web one thing we could do i. This form of the theorem relates the vector line integral over a. If p p and q q. A circulation form and a flux form. Web circulation form of green’s theorem. Web circulation form of green's theorem. In the flux form, the integrand is f · n. Web section 4.2 green's theorem (circulation form) green's theorem relates the circulation around a closed path (a global property) to the circulation density (a local.
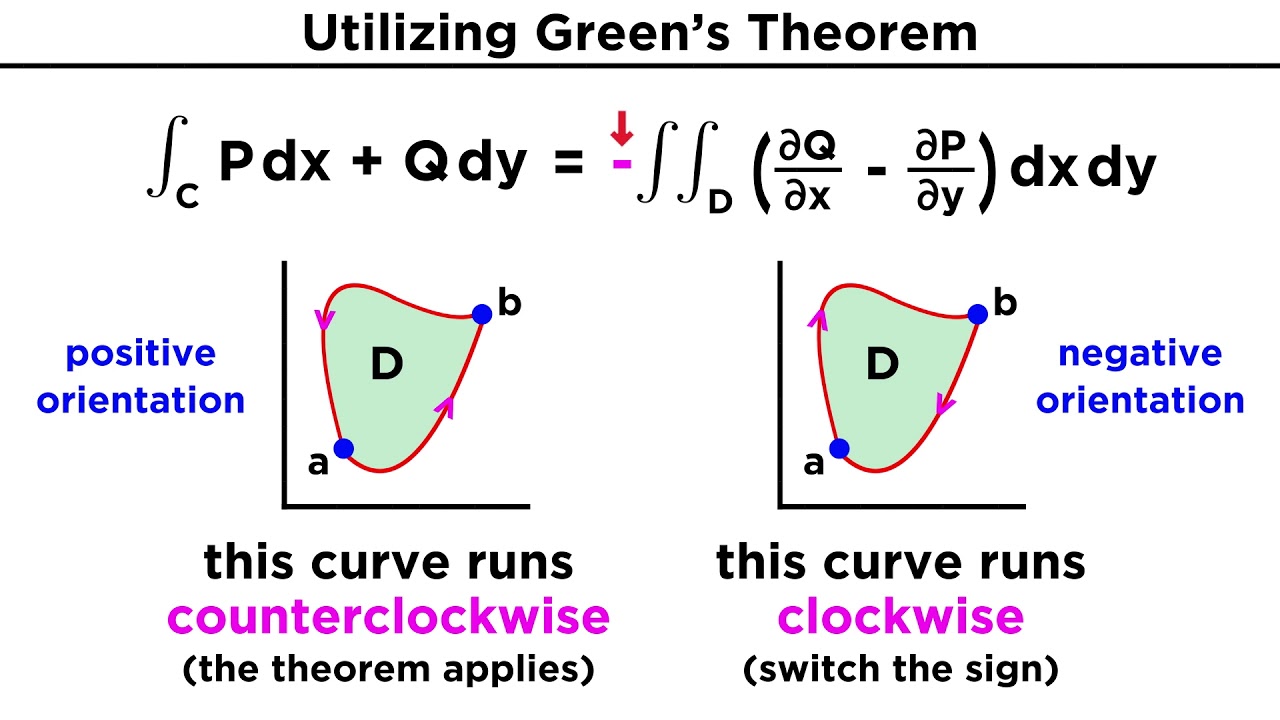
A circulation form and a flux form, both of which require region d in the double integral to be simply connected. Web green’s theorem let c c be a positively oriented, piecewise smooth, simple, closed curve and let d d be the region enclosed by the curve. In the circulation form, the integrand is f⋅t f ⋅ t. Web this marvelous fact is called green's theorem. In the flux form, the integrand is f⋅n f ⋅ n. The first form of green’s theorem that we examine is the circulation form. Web theorem let c be a positively oriented, piecewise smooth, simple closed curve in a plane, and let d be the region bounded by c. Math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem. A circulation form and a flux form. Web one thing we could do i.
Web green’s theorem comes in two forms: Web circulation form of green's theorem. However, we will extend green’s. Web one thing we could do i. Web theorem let c be a positively oriented, piecewise smooth, simple closed curve in a plane, and let d be the region bounded by c. Web section 4.2 green's theorem (circulation form) green's theorem relates the circulation around a closed path (a global property) to the circulation density (a local. It relates the line integral of a vector field around a planecurve to a double. A circulation form and a flux form. Web the circulation form of green’s theorem relates a line integral over curve c to a double integral over region d. In the flux form, the integrand is f⋅n f ⋅ n.
The stokes theorem uses which of the following operation
Web circulation form of green's theorem math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem © 2023 khan academy terms of use. Web green’s theorem comes in two forms: What is the meaning of. His video is all about green's theorem, or at least the first of two green's theorem sometimes called the curl, circulation,.
Green's Theorem (Circulation & Flux Forms with Examples) YouTube
Web green’s theorem let c c be a positively oriented, piecewise smooth, simple, closed curve and let d d be the region enclosed by the curve. This form of the theorem relates the vector line integral over a. Web one thing we could do i. Web this marvelous fact is called green's theorem. Math > multivariable calculus > green's, stokes',.
Green's Theorem, Circulation Form YouTube
Math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem. Notice that green’s theorem can be used only for a two. What is the meaning of. If p p and q q. Web the circulation form of green’s theorem relates a line integral over curve c to a double integral over region d.
multivariable calculus How are the two forms of Green's theorem are
In the flux form, the integrand is f⋅n f ⋅ n. A circulation form and a flux form. Web green’s theorem has two forms: In the circulation form, the integrand is f · t. The first form of green’s theorem that we examine is the circulation form.
Solved The Circulation Form Of Green's Theorem Relates A
Web circulation form of green's theorem math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem © 2023 khan academy terms of use. Web green’s theorem let c c be a positively oriented, piecewise smooth, simple, closed curve and let d d be the region enclosed by the curve. His video is all about green's theorem,.
Flux Form of Green's Theorem YouTube
In the flux form, the integrand is f · n. Practice green's theorem (articles) learn green's theorem green's theorem examples 2d. In the circulation form, the integrand is f⋅t f ⋅ t. Web this marvelous fact is called green's theorem. Web theorem let c be a positively oriented, piecewise smooth, simple closed curve in a plane, and let d be.
Determine the Flux of a 2D Vector Field Using Green's Theorem
What is the meaning of. Web circulation form of green's theorem math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem © 2023 khan academy terms of use. If l and m are functions of (x, y) defined on an. Web this marvelous fact is called green's theorem. This form of the theorem relates the vector.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
Practice green's theorem (articles) learn green's theorem green's theorem examples 2d. Web green’s theorem has two forms: Web the circulation form of green’s theorem relates a line integral over curve c to a double integral over region d. In the circulation form, the integrand is f · t. Web start circulation form of green's theorem get 3 of 4 questions.
Curl, Circulation, and Green's Theorem // Vector Calculus YouTube
Math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem. What is the meaning of. Web green’s theorem has two forms: In the flux form, the integrand is f · n. A circulation form and a flux form, both of which require region d in the double integral to be simply connected.
Green's Theorem YouTube
Web section 4.2 green's theorem (circulation form) green's theorem relates the circulation around a closed path (a global property) to the circulation density (a local. This form of the theorem relates the vector line integral over a. Notice that green’s theorem can be used only for a two. In the circulation form, the integrand is f⋅t f ⋅ t. Web.
Web Green’s Theorem Comes In Two Forms:
A circulation form and a flux form, both of which require region d in the double integral to be simply connected. In the circulation form, the integrand is f⋅t f ⋅ t. In the circulation form, the integrand is f · t. Math > multivariable calculus > green's, stokes', and the divergence theorems > green's theorem.
Web Green’s Theorem Let C C Be A Positively Oriented, Piecewise Smooth, Simple, Closed Curve And Let D D Be The Region Enclosed By The Curve.
Web green’s theorem comes in two forms: Web circulation form of green's theorem. Web the circulation form of green’s theorem relates a line integral over curve c to a double integral over region d. This form of the theorem relates the vector line integral over a.
Notice That Green’s Theorem Can Be Used Only For A Two.
Web circulation form of green’s theorem. However, we will extend green’s. Practice green's theorem (articles) learn green's theorem green's theorem examples 2d. His video is all about green's theorem, or at least the first of two green's theorem sometimes called the curl, circulation, or tangential form.
The First Form Of Green’s Theorem That We Examine Is The Circulation Form.
Web green’s theorem has two forms: Web start circulation form of green's theorem get 3 of 4 questions to level up! Web green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: A circulation form and a flux form.